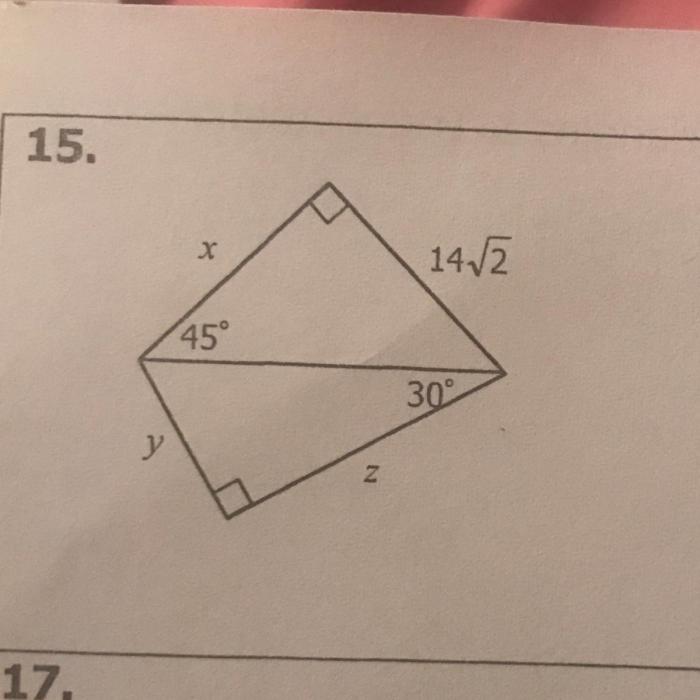
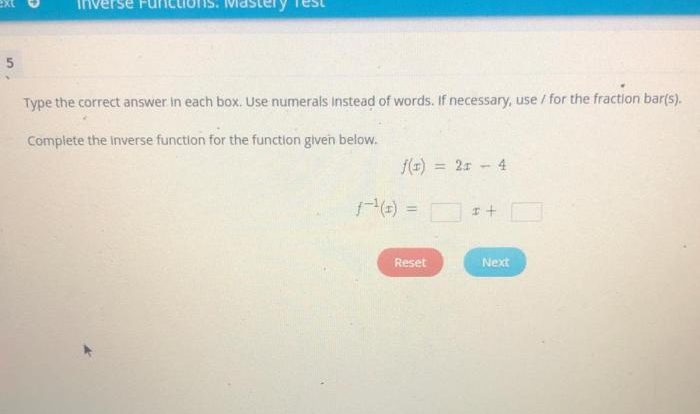
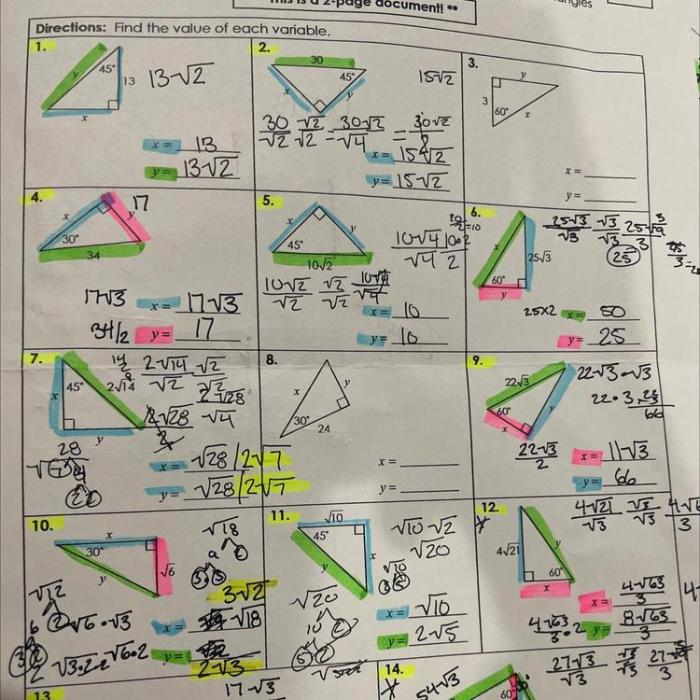
Unit 8 right triangles & trigonometry homework 4 – Unit 8: Right Triangles & Trigonometry Homework 4 embarks on an enlightening journey into the realm of trigonometry, unraveling the intricate relationships between the sides and angles of right triangles. Prepare to delve into a world of trigonometric ratios, right triangle problem-solving, and the practical applications of trigonometry in diverse fields.
Through engaging explanations, step-by-step examples, and real-world scenarios, this homework assignment empowers learners to master the concepts of trigonometry, equipping them with the tools to navigate the complexities of mathematics and its applications in the wider world.
Trigonometric Ratios
Trigonometry is the study of the relationships between the sides and angles of triangles. Trigonometric ratios are used to express these relationships. The three main trigonometric ratios are sine, cosine, and tangent.Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
Cosine is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. Tangent is defined as the ratio of the length of the opposite side to the length of the adjacent side.Trigonometric ratios can be used to solve a variety of problems involving right triangles.
For example, they can be used to find the length of a missing side, the measure of an angle, or the area of a triangle.
Solving Right Triangles
The Pythagorean theorem is a fundamental theorem of geometry that states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides.
This theorem can be used to solve a variety of problems involving right triangles.For example, it can be used to find the length of a missing side, the measure of an angle, or the area of a triangle.Trigonometric ratios can also be used to solve right triangles.
For example, they can be used to find the length of a missing side, the measure of an angle, or the area of a triangle.
Applications of Trigonometry
Trigonometry has a wide variety of applications in the real world. For example, it is used in architecture, engineering, and navigation.In architecture, trigonometry is used to calculate the heights of buildings, the lengths of bridges, and the angles of roofs.
In engineering, trigonometry is used to calculate the forces acting on structures, the trajectories of projectiles, and the efficiency of engines. In navigation, trigonometry is used to calculate the distances between objects, the courses of ships, and the positions of aircraft.Trigonometry
is also used in a variety of other fields, such as surveying, astronomy, and music.
Graphing Trigonometric Functions, Unit 8 right triangles & trigonometry homework 4
Trigonometric functions are periodic functions that can be graphed using a variety of techniques. The most common techniques are the unit circle and the sine and cosine curves.The unit circle is a circle with radius 1. The sine and cosine of an angle are defined as the y- and x-coordinates, respectively, of the point on the unit circle that corresponds to that angle.The
sine and cosine curves are the graphs of the sine and cosine functions, respectively. These curves are periodic with period 2π.Trigonometric functions can be transformed in a variety of ways. For example, they can be shifted, scaled, or reflected. These transformations can be used to create a variety of different graphs.
FAQs: Unit 8 Right Triangles & Trigonometry Homework 4
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
How do I find the sine of an angle?
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse.
What are the applications of trigonometry?
Trigonometry is used in a wide variety of fields, including architecture, engineering, navigation, and surveying.